Cone Clutch
Cone clutch with plates that engage when normal force exceeds threshold
Libraries:
Simscape /
Driveline /
Clutches
Description
The Cone Clutch block represents a friction clutch with a conical contact interface. The conical interface reduces the normal force required for clutch engagement by creating a wedging action between the clutch components, a cone and a cup. Cone clutch applications include synchromesh gearboxes, which synchronize the drive and driven shaft speeds to enable smoother engagement between transmission gears.
The cup component connects rigidly to the drive shaft, spinning with it as a unit. The cone component connects rigidly to the driven shaft, which sits in axial alignment with the drive shaft. The clutch engages when the cone slides toward the cup and presses tightly against its internal surface. Friction at the cone-cup contact interface enables the clutch to transmit rotational power between the drive and driven shafts. The friction model of this block includes both static and kinetic friction contributions, the latter of which leads to power dissipation during slip between the cone and cup components.
The Cone Clutch block is based on the Fundamental Friction Clutch block. For the complete friction clutch model, see Fundamental Friction Clutch. This section discusses the specialized model implemented in the Cone Clutch block.
When you apply a normal force, FN, the Cone Clutch block can apply two kinds of friction, kinetic and static, to the driveline motion. The clutch applies kinetic friction torque only when one driveline axis is spinning relative to the other driveline axis. The clutch applies static friction torque when the two driveline axes lock and spin together. The block iterates through multistep testing to determine when to lock and unlock the clutch.
Clutch Geometry and Variables
The figure shows the cone clutch geometry.
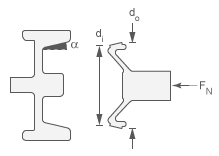
Clutch Variables
| Parameter | Definition | Significance |
|---|---|---|
| do | Outer diameter of the conical contact surface | See the preceding figure |
| di | Inner diameter of the conical contact surface | See the preceding figure |
| α | Cone half angle | See the preceding figure |
| ω | Relative angular velocity (slip) | ωF – ωB |
| ωTol | Slip tolerance for clutch locking | See the following model |
| FN | Normal force applied to conical surfaces | Normal force applied, if greater than threshold: FN > Fth |
| α | Cone half-angle | See the preceding figure |
| reff | Effective torque radius | Effective moment arm of clutch friction force |
| kK | Kinetic friction coefficient | Dimensionless coefficient of kinetic friction of conical friction surfaces. Function of ω. |
| kS | Static friction coefficient | Dimensionless coefficient of static friction of conical friction surfaces. |
| τK | Kinetic friction torque | See the following model |
| τS | Static friction torque limit | (static friction peak factor)·(kinetic
friction torque for ω → 0) (See the following model) |
Relation to Fundamental Friction Clutch
The Cone Clutch block is based on the Fundamental Friction Clutch block. Instead of requiring the kinetic and static friction limit torques as input signals, the Cone Clutch block calculates the kinetic and static friction from the clutch parameters and the input normal force signal FN.
The kinetic friction torque is the product of four factors:
The kinetic friction torque opposes the relative slip and is applied with an overall minus sign. It changes sign when ω changes sign.
You specify the kinetic friction coefficient, kK, as either a constant or a tabulated discrete function of relative angular velocity, ω. The tabulated function is assumed to be symmetric for positive and negative values of the relative angular velocity. Therefore, specify kK for positive values of ω only.
The effective torque radius, reff, is the effective radius, measured from the driveline axis, at which the kinetic friction forces are applied at the frictional surfaces. It is related to the geometry of the conical friction surface geometry by:
do and di are the contact surface maximum and minimum diameters, respectively.
The static friction limit is related to the kinetic friction, setting ω to zero and replacing the kinetic with the static friction coefficient:
kS > kK, so that the torque, τ, needed across the clutch to unlock it by overcoming static friction is larger than the kinetic friction at the instant of unlocking, when ω = 0.
The static friction limit defines symmetric static friction torque limits as:
The range [τS–, τS+] is used by the Fundamental Friction Clutch.
The clutch engages (transmits torque) when the conical friction surfaces are subject to a positive normal force and generate kinetic friction: FN > 0 and τK> 0.
The clutch locks if and only if it is engaged, and the slip is less than the velocity tolerance: |ω| < ωTol.
The power dissipated by the clutch is |ω·τK|. The clutch dissipates power only if it is both slipping (ω ≠ 0) and applying kinetic friction (τK > 0).
Velocity-Dependent Model
You can model the effects of rotational velocity change by selecting a
velocity-dependent model. To choose a velocity-dependent model, in
the Friction settings, set the
Friction model parameter to
Velocity-dependent kinetic friction
coefficient. For information about a friction
model that depends on both velocity and temperature, see Thermal, Velocity-Dependent Model.
Thermal Model
You can model the effects of heat flow and temperature change by
selecting a temperature-dependent model. To choose a
temperature-dependent model, in the Friction
settings, set the Friction model parameter to
Temperature-dependent friction
coefficients. For information about a friction
model that depends on both velocity and temperature, see Thermal, Velocity-Dependent Model.
Thermal, Velocity-Dependent Model
You can model the effects of rotational velocity change and heat flow
by selecting a velocity-dependent and temperature-dependent model.
To choose a model that depends on both velocity and temperature, in
the Friction settings, set the
Friction model parameter to
Temperature and velocity-dependent friction
coefficients.
Faults
To model a fault in the Cone Clutch block, in the Faults section, click the Add fault hyperlink next to the fault that you want to model. When the Add Fault window opens, you can to specify the fault properties. For more information about fault modeling, see Fault Behavior Modeling and Fault Triggering.
When you trigger a fault, the block responds according to the setting of the Behavior when faulted parameter for the remainder of the simulation. The fault options are:
Cannot transmit powerCannot unlock