Linear Frequency Modulated Pulse Waveforms
Benefits of Using Linear FM Pulse Waveform
Increasing the duration of a transmitted pulse increases its energy and improves target detection capability. Conversely, reducing the duration of a pulse improves the range resolution of the radar.
For a rectangular pulse, the duration of the transmitted pulse and the processed echo are effectively the same. Therefore, the range resolution of the radar and the target detection capability are coupled in an inverse relationship.
Pulse compression techniques enable you to decouple the duration of the pulse from its energy by effectively creating different durations for the transmitted pulse and processed echo. Using a linear frequency modulated pulse waveform is a popular choice for pulse compression.
Definition of Linear FM Pulse Waveform
The complex envelope of a linear FM pulse waveform with increasing instantaneous frequency is:
where β is the bandwidth and τ is the pulse duration.
If you denote the phase by Θ(t), the instantaneous frequency is:
which is a linear function of t with slope equal to β/τ.
The complex envelope of a linear FM pulse waveform with decreasing instantaneous frequency is:
Pulse compression waveforms have a time-bandwidth product, βτ, greater than 1.
How to Create Linear FM Pulse Waveforms
To create a linear FM pulse waveform, use phased.LinearFMWaveform.
You can customize certain characteristics of the waveform, including:
Sample rate
Duration of a single pulse
Pulse repetition frequency
Sweep bandwidth
Sweep direction (up or down), corresponding to increasing and decreasing instantaneous frequency
Envelope, which describes the amplitude modulation of the pulse waveform. The envelope can be rectangular or Gaussian.
The rectangular envelope is as follows, where τ is the pulse duration.
The Gaussian envelope is:
Number of samples or pulses in each vector that represents the waveform
Create Linear FM Pulse Waveform
This example shows how to create a linear FM pulse waveform using phased.LinearFMWaveform. The example illustrates how to specify property settings.
Create a linear FM pulse with a sample rate of 1 MHz, a pulse duration of 50 μs with an increasing instantaneous frequency, and a sweep bandwidth of 100 kHz. The pulse repetition frequency is 10 kHz and the amplitude modulation is rectangular.
waveform = phased.LinearFMWaveform('SampleRate',1e6,... 'PulseWidth',50e-6,'PRF',10e3,... 'SweepBandwidth',100e3,'SweepDirection','Up',... 'Envelope','Rectangular',... 'OutputFormat','Pulses','NumPulses',1);
Linear FM Pulse Waveform Plot
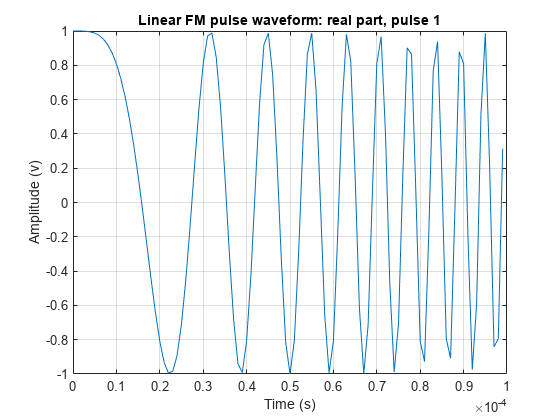
This example shows how to plot a linear FM (LFM) pulse waveform. The LFM waveform has a duration of 100 microseconds, a bandwidth of 200 kHz, and a PRF of 4 kHz. Use the default values for the other properties. Compute the time-bandwidth product. Plot the real part of the waveform and plot one full pulse repetition interval.
waveform = phased.LinearFMWaveform('PulseWidth',100e-6,... 'SweepBandwidth',200e3,'PRF',4e3);
Display the time-bandwidth product of the FM sweep.
disp(waveform.PulseWidth*waveform.SweepBandwidth)
20
Plot the real part of the waveform.
plot(waveform)
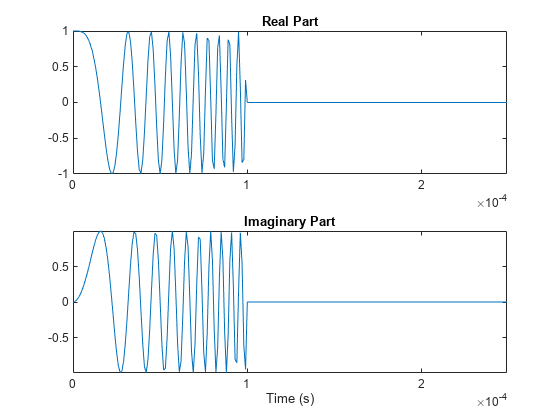
Use the step method to obtain one full repetition interval of the signal. Plot the real and imaginary parts.
y = waveform(); t = unigrid(0,1/waveform.SampleRate,1/waveform.PRF,'[)'); figure subplot(2,1,1) plot(t,real(y)) axis tight title('Real Part') subplot(2,1,2) plot(t,imag(y)) xlabel('Time (s)') title('Imaginary Part') axis tight
Ambiguity Function of Linear FM Waveform
This example shows how to plot the ambiguity function of a linear FM pulse waveform.
Define and set up the linear FM waveform.
waveform = phased.LinearFMWaveform('PulseWidth',100e-6,... 'SweepBandwidth',2e5,'PRF',1e3);
Generate samples of the waveform.
wav = waveform();
Create a 3-D surface plot of the ambiguity function for the waveform.
[afmag_lfm,delay_lfm,doppler_lfm] = ambgfun(wav,... waveform.SampleRate,waveform.PRF); surf(delay_lfm*1e6,doppler_lfm/1e3,afmag_lfm,... 'LineStyle','none') axis tight grid on view([140,35]) colorbar xlabel('Delay \tau (\mus)') ylabel('Doppler f_d (kHz)') title('Linear FM Pulse Waveform Ambiguity Function')
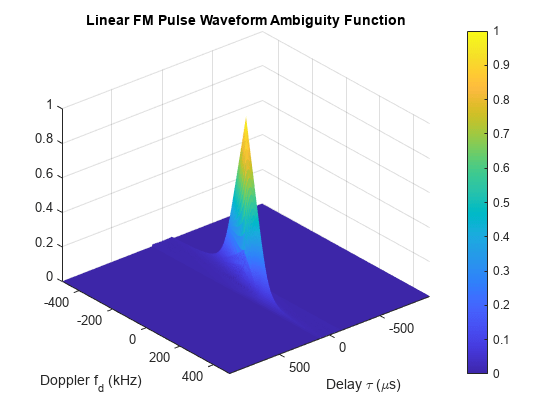
The surface has a narrow ridge that is slightly tilted. The tilt indicates better resolution in the zero delay cut.
Compare Autocorrelation for Rectangular and Linear FM Waveforms
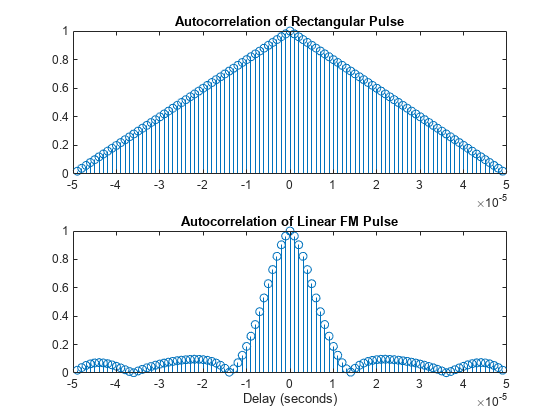
This example shows how to compute and plot the ambiguity function magnitudes for a rectangular and linear FM pulse waveform. The zero Doppler cut (magnitudes of the autocorrelation sequences) illustrates pulse compression in the linear FM pulse waveform.
Create a rectangular waveform and a linear FM pulse waveform having the same duration and PRF. Generate samples of each waveform.
rectwaveform = phased.RectangularWaveform('PRF',20e3); lfmwaveform = phased.LinearFMWaveform('PRF',20e3); xrect = rectwaveform(); xlfm = lfmwaveform();
Compute the ambiguity function magnitudes for each waveform.
[ambrect,delay] = ambgfun(xrect,rectwaveform.SampleRate,rectwaveform.PRF,... 'Cut','Doppler'); ambfm = ambgfun(xlfm,lfmwaveform.SampleRate,lfmwaveform.PRF,... 'Cut','Doppler');
Plot the ambiguity function magnitudes.
subplot(211) stem(delay,ambrect) title('Autocorrelation of Rectangular Pulse') axis([-5e-5 5e-5 0 1]) set(gca,'XTick',1e-5*(-5:5)) subplot(212) stem(delay,ambfm) xlabel('Delay (seconds)') title('Autocorrelation of Linear FM Pulse') axis([-5e-5 5e-5 0 1]) set(gca,'XTick',1e-5*(-5:5))