Minimal Surface Problem
This example shows how to solve the minimal surface equation
on the unit disk , with on the boundary . An elliptic equation in the toolbox form is
.
Therefore, for the minimal surface problem, the coefficients are:
.
Because the coefficient c is a function of the solution u, the minimal surface problem is a nonlinear elliptic problem.
To solve the minimal surface problem using the programmatic workflow, first create a PDE model with a single dependent variable.
model = createpde;
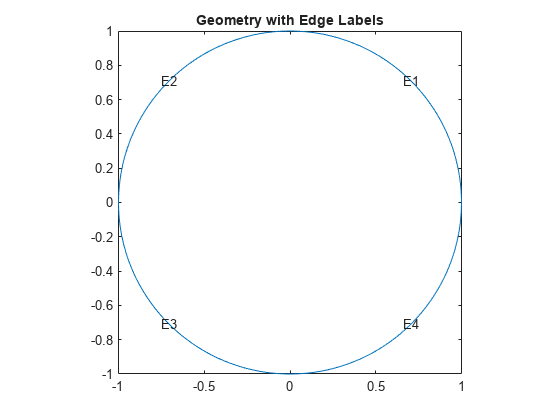
Create the geometry and include it in the model. The circleg function represents this geometry.
geometryFromEdges(model,@circleg);
Plot the geometry with the edge labels.
pdegplot(model,"EdgeLabels","on") axis equal title("Geometry with Edge Labels")
Specify the coefficients.
a = 0; f = 0; cCoef = @(region,state) 1./sqrt(1+state.ux.^2 + state.uy.^2); specifyCoefficients(model,"m",0,"d",0,"c",cCoef,"a",a,"f",f);
Specify the boundary conditions using the function .
bcMatrix = @(region,~)region.x.^2; applyBoundaryCondition(model,"dirichlet", ... "Edge",1:model.Geometry.NumEdges, ... "u",bcMatrix);
Generate and plot a mesh.
generateMesh(model,"Hmax",0.1); figure; pdemesh(model); axis equal

Clear figure for future plots.
clf
Solve the problem by using the solvepde function. Because the problem is nonlinear, solvepde invokes a nonlinear solver. Observe the solver progress by setting the SolverOptions.ReportStatistics property of the model to 'on'.
model.SolverOptions.ReportStatistics = 'on';
result = solvepde(model);Iteration Residual Step size Jacobian: Full 0 1.8532e-02 1 2.8391e-04 1.0000000 2 1.1738e-06 1.0000000
u = result.NodalSolution;
Plot the solution by using the Visualize PDE Results Live Editor task. First, create a new live script by clicking the New Live Script button in the File section on the Home tab.
On the Live Editor tab, select Task > Visualize PDE Results. This action inserts the task into your script.
To plot the solution, follow these steps.
In the Select results section of the task, select
resultfrom the drop-down list.In the Specify data parameters section of the task, set Type to Nodal solution.
In the Specify visualization parameters section of the task, select the Mesh check box.
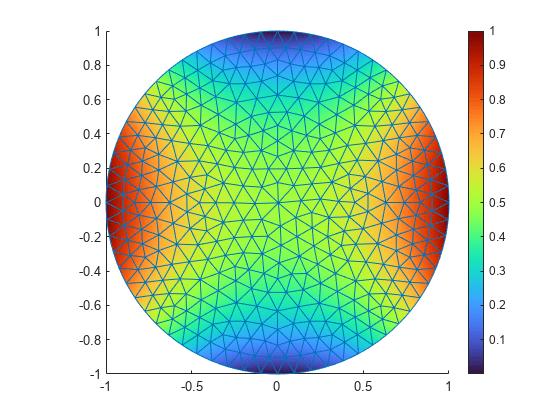
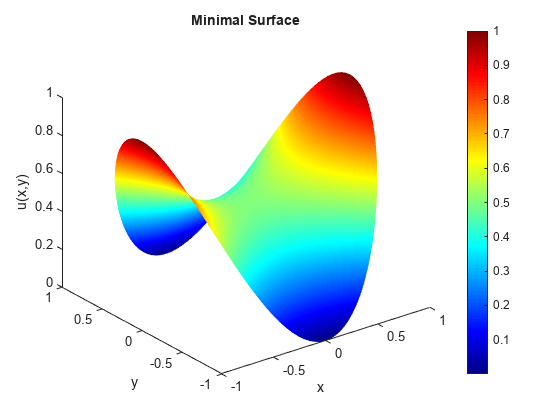
You also can plot the solution at the MATLAB® command line by using the pdeplot function. For example, plot the solution as a 3-D plot, using the solution values for plot heights.
figure; pdeplot(model,"XYData",u,"ZData",u); xlabel x ylabel y zlabel u(x,y) title("Minimal Surface") colormap jet