Nonlinear Data-Fitting
This example shows how to fit a nonlinear function to data using several Optimization Toolbox™ algorithms.
Problem Setup
Consider the following data:
Data = ...
[0.0000 5.8955
0.1000 3.5639
0.2000 2.5173
0.3000 1.9790
0.4000 1.8990
0.5000 1.3938
0.6000 1.1359
0.7000 1.0096
0.8000 1.0343
0.9000 0.8435
1.0000 0.6856
1.1000 0.6100
1.2000 0.5392
1.3000 0.3946
1.4000 0.3903
1.5000 0.5474
1.6000 0.3459
1.7000 0.1370
1.8000 0.2211
1.9000 0.1704
2.0000 0.2636];Let's plot these data points.
t = Data(:,1); y = Data(:,2); % axis([0 2 -0.5 6]) % hold on plot(t,y,'ro') title('Data points')
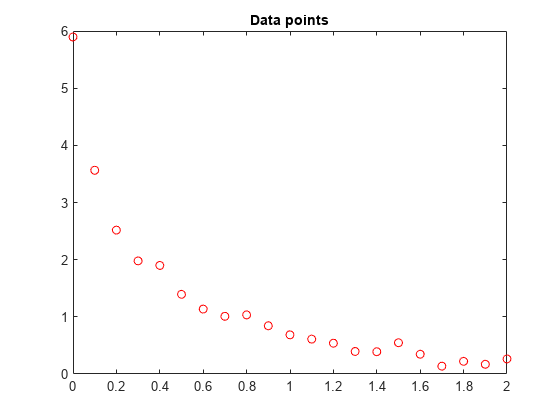
% hold offWe would like to fit the function
y = c(1)*exp(-lam(1)*t) + c(2)*exp(-lam(2)*t)
to the data.
Solution Approach Using lsqcurvefit
The lsqcurvefit function solves this type of problem easily.
To begin, define the parameters in terms of one variable x:
x(1) = c(1)
x(2) = lam(1)
x(3) = c(2)
x(4) = lam(2)
Then define the curve as a function of the parameters x and the data t:
F = @(x,xdata)x(1)*exp(-x(2)*xdata) + x(3)*exp(-x(4)*xdata);
We arbitrarily set our initial point x0 as follows: c(1) = 1, lam(1) = 1, c(2) = 1, lam(2) = 0:
x0 = [1 1 1 0];
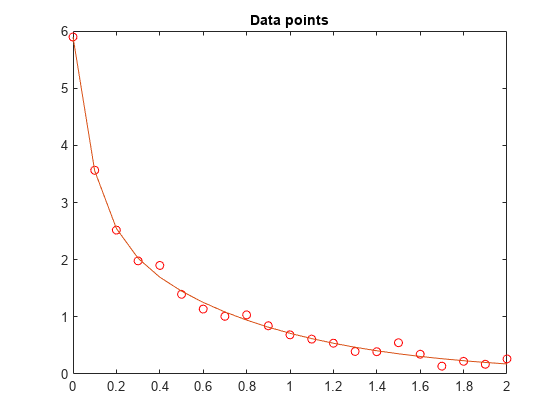
We run the solver and plot the resulting fit.
[x,resnorm,~,exitflag,output] = lsqcurvefit(F,x0,t,y)
Local minimum possible. lsqcurvefit stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
x = 1×4
3.0068 10.5869 2.8891 1.4003
resnorm = 0.1477
exitflag = 3
output = struct with fields:
firstorderopt: 7.8830e-06
iterations: 6
funcCount: 35
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 0.0096
message: 'Local minimum possible....'
bestfeasible: []
constrviolation: []
hold on plot(t,F(x,t)) hold off
Solution Approach Using fminunc
To solve the problem using fminunc, we set the objective function as the sum of squares of the residuals.
Fsumsquares = @(x)sum((F(x,t) - y).^2); opts = optimoptions('fminunc','Algorithm','quasi-newton'); [xunc,ressquared,eflag,outputu] = ... fminunc(Fsumsquares,x0,opts)
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance.
xunc = 1×4
2.8890 1.4003 3.0069 10.5862
ressquared = 0.1477
eflag = 1
outputu = struct with fields:
iterations: 30
funcCount: 185
stepsize: 0.0017
lssteplength: 1
firstorderopt: 2.9662e-05
algorithm: 'quasi-newton'
message: 'Local minimum found....'
Notice that fminunc found the same solution as lsqcurvefit, but took many more function evaluations to do so. The parameters for fminunc are in the opposite order as those for lsqcurvefit; the larger lam is lam(2), not lam(1). This is not surprising, the order of variables is arbitrary.
fprintf(['There were %d iterations using fminunc,' ... ' and %d using lsqcurvefit.\n'], ... outputu.iterations,output.iterations)
There were 30 iterations using fminunc, and 6 using lsqcurvefit.
fprintf(['There were %d function evaluations using fminunc,' ... ' and %d using lsqcurvefit.'], ... outputu.funcCount,output.funcCount)
There were 185 function evaluations using fminunc, and 35 using lsqcurvefit.
Splitting the Linear and Nonlinear Problems
Notice that the fitting problem is linear in the parameters c(1) and c(2). This means for any values of lam(1) and lam(2), we can use the backslash operator to find the values of c(1) and c(2) that solve the least-squares problem.
We now rework the problem as a two-dimensional problem, searching for the best values of lam(1) and lam(2). The values of c(1) and c(2) are calculated at each step using the backslash operator as described above.
type fitvectorfunction yEst = fitvector(lam,xdata,ydata) %FITVECTOR Used by DATDEMO to return value of fitting function. % yEst = FITVECTOR(lam,xdata) returns the value of the fitting function, y % (defined below), at the data points xdata with parameters set to lam. % yEst is returned as a N-by-1 column vector, where N is the number of % data points. % % FITVECTOR assumes the fitting function, y, takes the form % % y = c(1)*exp(-lam(1)*t) + ... + c(n)*exp(-lam(n)*t) % % with n linear parameters c, and n nonlinear parameters lam. % % To solve for the linear parameters c, we build a matrix A % where the j-th column of A is exp(-lam(j)*xdata) (xdata is a vector). % Then we solve A*c = ydata for the linear least-squares solution c, % where ydata is the observed values of y. A = zeros(length(xdata),length(lam)); % build A matrix for j = 1:length(lam) A(:,j) = exp(-lam(j)*xdata); end c = A\ydata; % solve A*c = y for linear parameters c yEst = A*c; % return the estimated response based on c
Solve the problem using lsqcurvefit, starting from a two-dimensional initial point lam(1), lam(2):
x02 = [1 0]; F2 = @(x,t) fitvector(x,t,y); [x2,resnorm2,~,exitflag2,output2] = lsqcurvefit(F2,x02,t,y)
Local minimum possible. lsqcurvefit stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
x2 = 1×2
10.5861 1.4003
resnorm2 = 0.1477
exitflag2 = 3
output2 = struct with fields:
firstorderopt: 4.4087e-06
iterations: 10
funcCount: 33
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 0.0080
message: 'Local minimum possible....'
bestfeasible: []
constrviolation: []
The efficiency of the two-dimensional solution is similar to that of the four-dimensional solution:
fprintf(['There were %d function evaluations using the 2-d ' ... 'formulation, and %d using the 4-d formulation.'], ... output2.funcCount,output.funcCount)
There were 33 function evaluations using the 2-d formulation, and 35 using the 4-d formulation.
Split Problem is More Robust to Initial Guess
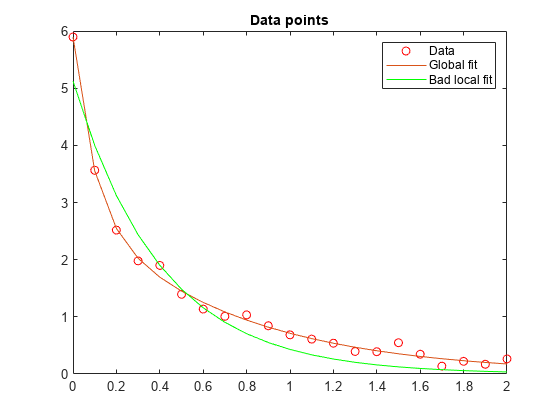
Choosing a bad starting point for the original four-parameter problem leads to a local solution that is not global. Choosing a starting point with the same bad lam(1) and lam(2) values for the split two-parameter problem leads to the global solution. To show this we re-run the original problem with a start point that leads to a relatively bad local solution, and compare the resulting fit with the global solution.
x0bad = [5 1 1 0];
[xbad,resnormbad,~,exitflagbad,outputbad] = ...
lsqcurvefit(F,x0bad,t,y)Local minimum possible. lsqcurvefit stopped because the final change in the sum of squares relative to its initial value is less than the value of the function tolerance.
xbad = 1×4
-22.9036 2.4792 28.0273 2.4791
resnormbad = 2.2173
exitflagbad = 3
outputbad = struct with fields:
firstorderopt: 0.0056
iterations: 32
funcCount: 165
cgiterations: 0
algorithm: 'trust-region-reflective'
stepsize: 0.0021
message: 'Local minimum possible....'
bestfeasible: []
constrviolation: []
hold on plot(t,F(xbad,t),'g') legend('Data','Global fit','Bad local fit','Location','NE') hold off
fprintf(['The residual norm at the good ending point is %f,' ... ' and the residual norm at the bad ending point is %f.'], ... resnorm,resnormbad)
The residual norm at the good ending point is 0.147723, and the residual norm at the bad ending point is 2.217300.
