fzero
Root of nonlinear function
Syntax
Description
Examples
Root Starting From One Point
Calculate by finding the zero of the sine function near 3.
fun = @sin; % function x0 = 3; % initial point x = fzero(fun,x0)
x = 3.1416
Root Starting from an Interval
Find the zero of cosine between 1 and 2.
fun = @cos; % function x0 = [1 2]; % initial interval x = fzero(fun,x0)
x = 1.5708
Note that and differ in sign.
Root of a Function Defined by a File
Find a zero of the function f(x) = x3 – 2x – 5.
First, write a file called f.m.
function y = f(x)
y = x.^3 - 2*x - 5;Save f.m on your MATLAB® path.
Find the zero of f(x)
near 2.
fun = @f; % function x0 = 2; % initial point z = fzero(fun,x0)
z =
2.0946Since f(x) is a polynomial, you can
find the same real zero, and a complex conjugate pair of zeros, using
the roots command.
roots([1 0 -2 -5])
ans = 2.0946 -1.0473 + 1.1359i -1.0473 - 1.1359i
Root of Function with Extra Parameter
Find the root of a function that has an extra parameter.
myfun = @(x,c) cos(c*x); % parameterized function c = 2; % parameter fun = @(x) myfun(x,c); % function of x alone x = fzero(fun,0.1)
x = 0.7854
Nondefault Options
Plot the solution process by setting some plot functions.
Define the function and initial point.
fun = @(x)sin(cosh(x)); x0 = 1;
Examine the solution process by setting options that include plot functions.
options = optimset('PlotFcns',{@optimplotx,@optimplotfval});Run fzero including options.
x = fzero(fun,x0,options)
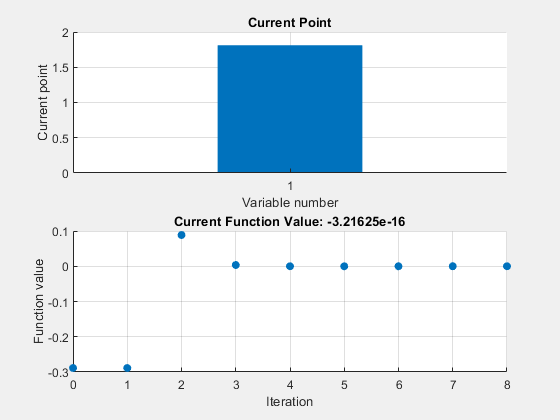
x = 1.8115
Solve Problem Structure
Solve a problem that is defined by a problem structure.
Define a structure that encodes a root-finding problem.
problem.objective = @(x)sin(cosh(x)); problem.x0 = 1; problem.solver = 'fzero'; % a required part of the structure problem.options = optimset(@fzero); % default options
Solve the problem.
x = fzero(problem)
x = 1.8115
More Information from Solution
Find the point where exp(-exp(-x)) = x, and display information about the solution process.
fun = @(x) exp(-exp(-x)) - x; % function x0 = [0 1]; % initial interval options = optimset('Display','iter'); % show iterations [x fval exitflag output] = fzero(fun,x0,options)
Func-count x f(x) Procedure
2 1 -0.307799 initial
3 0.544459 0.0153522 interpolation
4 0.566101 0.00070708 interpolation
5 0.567143 -1.40255e-08 interpolation
6 0.567143 1.50013e-12 interpolation
7 0.567143 0 interpolation
Zero found in the interval [0, 1]
x = 0.5671
fval = 0
exitflag = 1
output = struct with fields:
intervaliterations: 0
iterations: 5
funcCount: 7
algorithm: 'bisection, interpolation'
message: 'Zero found in the interval [0, 1]'
fval = 0 means fun(x) = 0, as desired.
Input Arguments
fun — Function to solve
function handle | function name
Function to solve, specified as a handle to a scalar-valued function or
the name of such a function. fun accepts a scalar
x and returns a scalar
fun(x).
fzero solves fun(x) = 0.
To solve an equation fun(x) = c(x), instead solve
fun2(x) = fun(x) - c(x) = 0.
To include extra parameters in your function, see the example Root of Function with Extra Parameter and the section Parameterizing Functions.
Example: 'sin'
Example: @myFunction
Example: @(x)(x-a)^5 - 3*x + a - 1
Data Types: char | function_handle | string
x0 — Initial value
scalar | 2-element vector
Initial value, specified as a real scalar or a 2-element real vector.
Scalar —
fzerobegins atx0and tries to locate a pointx1wherefun(x1)has the opposite sign offun(x0). Thenfzeroiteratively shrinks the interval wherefunchanges sign to reach a solution.2-element vector —
fzerochecks thatfun(x0(1))andfun(x0(2))have opposite signs, and errors if they do not. It then iteratively shrinks the interval wherefunchanges sign to reach a solution. An intervalx0must be finite; it cannot contain ±Inf.
Tip
Calling fzero with an interval (x0 with
two elements) is often faster than calling it with a scalar x0.
Example: 3
Example: [2,17]
Data Types: double
options — Options for solution process
structure, typically created using optimset
Options for solution process, specified as a structure. Create or modify
the options structure using optimset.
fzero uses these options structure
fields.
| Level of display:
|
| Check whether objective function values are valid.
|
| Specify one or more
user-defined functions that an optimization function
calls at each iteration, either as a function handle
or as a cell array of function handles. The default
is none ( |
| Plots various measures of
progress while the algorithm executes. Select from
predefined plots or write your own. Pass a function
name, function handle, or a cell array of function
names or handles. The default is none
(
For information on writing a custom plot function, see Optimization Solver Plot Functions. |
| Termination tolerance on
|
Example: options =
optimset('FunValCheck','on')
Data Types: struct
problem — Root-finding problem
structure
Root-finding problem, specified as a structure with all of the following fields.
| Objective function |
| Initial point for x,
real scalar or 2-element vector |
| 'fzero' |
| Options structure, typically created
using optimset |
For an example, see Solve Problem Structure.
Data Types: struct
Output Arguments
x — Location of root or sign change
real scalar
Location of root or sign change, returned as a scalar.
fval — Function value at x
real scalar
Function value at x, returned as a scalar.
exitflag — Integer encoding the exit condition
integer
Integer encoding the exit condition, meaning the reason fzero stopped
its iterations.
| Function converged to a solution |
| Algorithm was terminated by the output function or plot function. |
|
|
-4 | Complex function value was encountered while searching for an interval containing a sign change. |
-5 | Algorithm might have converged to a singular point. |
-6 |
|
output — Information about root-finding process
structure
Information about root-finding process, returned as a structure. The fields of the structure are:
intervaliterations | Number of iterations taken to find an interval containing a root |
iterations | Number of zero-finding iterations |
funcCount | Number of function evaluations |
algorithm |
|
message | Exit message |
Algorithms
The fzero command
is a function file. The algorithm, created by T. Dekker,
uses a combination of bisection, secant, and inverse quadratic interpolation
methods. An Algol 60 version, with some improvements, is given in [1]. A Fortran version, upon which fzero is
based, is in [2].
Alternative Functionality
App
The Optimize Live Editor task provides a visual interface for
fzero.
References
[1] Brent, R., Algorithms for Minimization Without Derivatives, Prentice-Hall, 1973.
[2] Forsythe, G. E., M. A. Malcolm, and C. B. Moler, Computer Methods for Mathematical Computations, Prentice-Hall, 1976.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
For C/C++ code generation:
The
funinput argument must be a function handle, and not a structure or character vector.fzeroignores all options except forTolXandFunValCheck.fzerodoes not support the fourth output argument, the output structure.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)