Compare GARCH Models Using Likelihood Ratio Test
This example shows how to conduct a likelihood ratio test to choose the number of lags in a GARCH model.
Load Data
Load the Deutschmark/British pound foreign-exchange rate data included with the toolbox. Convert the daily rates to returns.
load Data_MarkPound Y = Data; r = price2ret(Y); N = length(r); figure plot(r) xlim([0,N]) title('Mark-Pound Exchange Rate Returns')
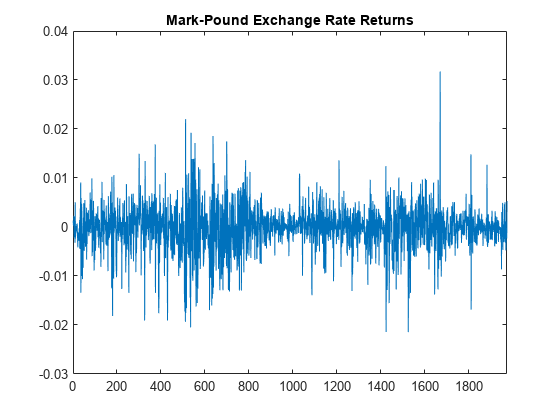
The daily returns exhibit volatility clustering. Large changes in the returns tend to cluster together, and small changes tend to cluster together. That is, the series exhibits conditional heteroscedasticity.
The returns are of relatively high frequency. Therefore, the daily changes can be small. For numerical stability, scale the data to percentage returns.
r = 100*r;
Fit GARCH(1,1) Model
Create and fit a GARCH(1,1) model (with a mean offset) to the returns series. Return the value of the loglikelihood objective function.
Mdl1 = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1); [EstMdl1,~,logL1] = estimate(Mdl1,r);
GARCH(1,1) Conditional Variance Model with Offset (Gaussian Distribution):
Value StandardError TStatistic PValue
__________ _____________ __________ __________
Constant 0.010761 0.001323 8.1342 4.1454e-16
GARCH{1} 0.80597 0.01656 48.669 0
ARCH{1} 0.15313 0.013974 10.959 6.0379e-28
Offset -0.0061904 0.0084336 -0.73402 0.46294
Fit GARCH(2,1) Model
Create and fit a GARCH(2,1) model with a mean offset.
Mdl2 = garch(2,1); Mdl2.Offset = NaN; [EstMdl2,~,logL2] = estimate(Mdl2,r);
GARCH(2,1) Conditional Variance Model with Offset (Gaussian Distribution):
Value StandardError TStatistic PValue
__________ _____________ __________ __________
Constant 0.011226 0.001538 7.2992 2.8947e-13
GARCH{1} 0.48964 0.11159 4.3878 1.1453e-05
GARCH{2} 0.29769 0.10218 2.9133 0.0035759
ARCH{1} 0.16842 0.016583 10.156 3.1158e-24
Offset -0.0049837 0.0084765 -0.58795 0.55657
Conduct Likelihood Ratio Test
Conduct a likelihood ratio test to compare the restricted GARCH(1,1) model fit to the unrestricted GARCH(2,1) model fit. The degree of freedom for this test is one (the number of restrictions).
[h,p] = lratiotest(logL2,logL1,1)
h = logical
1
p = 0.0218
At the 0.05 significance level, the null GARCH(1,1) model is rejected (h = 1) in favor of the unrestricted GARCH(2,1) alternative.
See Also
Objects
Functions
Related Examples
- Conduct Lagrange Multiplier Test
- Conduct Wald Test
- Compare Conditional Variance Models Using Information Criteria
